Código BCD a Decimal

Código BCD a Decimal

Para poder compartir información, que está en formato digital, es común utilizar las representaciones binaria y hexadecimal. Hay otros métodos de representar información y una de ellas es el código BCD. Con ayuda de la codificación BCD es más fácil ver la relación que hay  entre un número decimal (base 10) y el número correspondiente en binario (base 2)

El código BCD utiliza 4 dígitos binarios (ver en los dos ejemplos que siguen) para representar un dígito decimal (0 al 9). Cuando se hace conversión de binario a decimal típica no hay una directa relación entre el dígito decimal y el dígito binario.

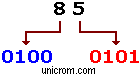
Ejemplo 1: Conversión directa típica entre un número en decimal y uno binario. 8510 = 10101012. La representación el mismo número decimal en código BCD se muestra a la derecha.

Ejemplo 2: Conversión directa típica entre un número en decimal y uno binario. 56810 = 10001110002. La representación el mismo número decimal en código BCD se muestra a la derecha.

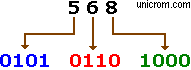
Como se puede ver, de los dos ejemplos anteriores, el número equivalente decimal no se parece a la representación en código BDC. Para poder obtener el equivalente código BCD de cada cifra de los números anteriores, se asigna un “peso” o “valor” según la posición que ocupa. Este “peso” o “valor” sigue el siguiente orden: 8 – 4 – 2 – 1. (Es un código ponderado). Del último ejemplo se observa que el número 5 se representa como: 0 1 0 1.

El primer “0” corresponde al 8, el primer “1” corresponde a 4, el segundo “0” corresponde a 2, y… el segundo “1” corresponde a 1. De lo anterior: 0 x 8 + 1 x 4 + 0 x 2 + 1 x 1 = 5

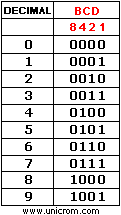
Al código BCD que tiene los “pesos” o “valores” antes descritos se le llama: Código BCD natural. El código BCD cuenta como un número binario normal del 0 al 9, pero del diez (1010) al quince (1111) no son permitidos pues no existen, para estos números, el equivalente de una cifra en decimal. Este código es utilizado, entre otras aplicaciones, para la representación de las cifras de los números decimales en displays de 7 segmentos.

Ya que cada grupo de 4 bits solo puede representar a un único dígito decimal, la conversión de un numero decimal a un numero BCD se lleva a cabo de la siguiente forma:
1. Separamos al dígito decimal en cada uno de sus dígitos2. Cada dígito decimal se transforma a su equivalente BCD.3. El número obtenido es el equivalente en BCD del número decimal.
Por ejemplo, para convertir el decimal 463 a BCD, según lo explicado anteriormente, tenemos que tomar cada dígito decimal y transformarlo a su equivalente BCD.

De esta forma el decimal 463 equivale al BCD 010001100011.

NOTA: En BCD los códigos 1010, 1011, 1100, 1101 y 1111 no tienen decimales equivalentes. Por lo tanto se les llaman códigos inválidos.